Trazar un poligono con un compas

Construcción de polígonos mediante el compás.

Mediante la aplicación de los conceptos referentes a los ángulos de los polígonos, es posible servirse del instrumento de dibujo que es el compás, para construir graficamente diversos polígonos.

El compás es un instrumento básicamente aplicable en el trazado de circunferencias, que delimitan una figura plana que es el círculo; el cual puede ser considerado un tipo especial de polígono regular, en el cual todos sus lados están constituídos solamente por un punto, y cuya dimensión está determinada por la longitud del radio, que es equivalente a la abertura del compás.

El método a utilizar para construir polígonos mediante el uso del compás, se basa en determinar los vértices de los lados del polígono, estableciendo en qué puntos de la circunsferencia deben situarse para que el polígono resulte inscripto en ella.

Esa determinación se realiza a partir del conocimiento de los valores de los ángulos centrales del polígono que se desea construir.

---

Para trazar un triángulo equilátero inscripto en un círculo, manteniendo el radio (abertura del compás) empleado para trazar el círculo, se determina un punto de la circunferencia (preferiblemente en la vertical inferior de su centro), y centrando en ese punto se traza un arco con extremos en la circunsferencia. Los puntos de intersección (A y B) determinan un lado del triángulo equilátero; por lo cual tomando la medida de ese segmento con el compás y trasladándola sobre la parte superior de la circunferencia, se determinará el vértice (C) de unión de los otros dos lados.

Ir al principio

---

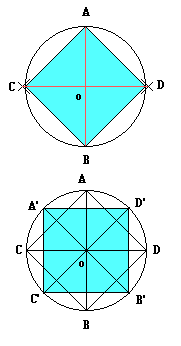Para trazar un cuadrado inscripto en un círculo, se traza una recta que pasando por el centro llegue a la circunsferencia en sus extremos (diámetro AB). Con una abertura del compás mayor a la empleada para trazar el círculo, centrando en los puntos extremos del diámetro, se marcan puntos en la circunferencia; lo que determinará dos nuevos puntos (C y D). Uniéndolos mediante una recta, resultará un nuevo diámetro perpendicular al anterior; cuyos puntos de contacto con la circunferencia serán los vértices del cuadrado inscripto. Como el cuadrado inscripto queda en posición transversal, puede trazarse otro con los lados en posición horizontal y vertical, simplemente trazando las medianas del cuadrado anterior, para determinar los vértices A', B', C' y D', de un nuevo cuadrado inscripto en el mismo círculo.

---

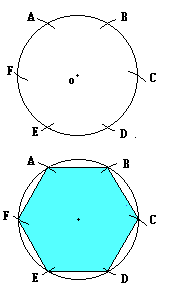Para trazar un hexágono inscripto en un círculo, se fija un punto sobre la circunferencia, y con la misma abertura del compás, se marcan puntos haciendo centro primero en ese punto y luego sucesivamente en los nuevos puntos. Ello determinará que se marquen sobre la circunferencia los seis puntos que corresponden a los vértices del hexágono. trazos con compás

PORCENTAJES

Video porcentaje

La palabra porcentaje, como indica su nombre, se refiere al número de partes que nos interesan de un total de 100. Por ejemplo, si existen 5470 establecimientos educacionales con enseñanza básica en el país (datos de 1999) y de ellos 1393 atienden a población rural, la fracción de establecimientos con enseñanza básica que atienden a la población rural es:

Podemos decir entonces que de cada 100 establecimientos con enseñanza básica aproximadamente 25 atienden a población rural.

Se puede trabajar de varias maneras con los porcentajes:

a.- Porcentaje como fracción:

"El 25 % de C es igual a ". Luego el 25% es igual a como fracción.

b.- Porcentaje como decimal
 

"El 25 % de C es igual a ". Luego 25 % es equivalente a 0.25 como número decimal.

Variación Proporcional mediante tablas y graficas

Las tablas de variación proporcional corresponden a aquellas en las que las cantidades aumentan o disminuyen de manera equivalente. Si una aumenta, la otra también lo hará.
 

     En la variación no proporcional, las cantidades que se relacionan no cambian proporcionalmente entre sí, mientras una aumenta, la otra disminuye.

     Las tablas y gráficas son estructuras que permiten presentar conjuntos de datos para que sea posible apreciar sus relaciones, realizar comparaciones y predecir tendencias. Las tablas se aplican a datos más o menos estables y las gráficas, a datos que tienen variaciones frecuentes.

     Ejemplo:

     En el taller mecánico donde Pancho trabaja, le pidieron que elaborara la cera para los automóviles de acuerdo con la siguiente fórmula: 82.50 g de cera de ceresina, 2 cucharadas de cera amarilla de abeja, 165 ml de aguarrás, 1 cucharada de aceite de pino.

¿Cuánta cera se necesita si se tienen las siguientes cantidades de aguarrás?

Aguarrás	165	330	495	660	825	990
Cera	82.50	165	247.50	330	412.50	495

   

  Después de hacer estos cálculos, Pancho necesita tenerlos siempre a la vista, para ello elaboró la siguiente gráfica.

Pancho quiere saber cuál es el tiempo mínimo de lavado de auto que ocuparían 6 empleados, si uno tarda 60 minutos.

Empleados	1	2	3	4	5	6
Tiempo	60	30	20	15	12	10

A continuación les presentare un video de como enseñar este tema. video variación proporcionalvideo variacion proporcional II